Sequoyah and the Almost-Forgotten History of Cherokee Numerals

By 1828, Sequoyah was at the peak of his renown. His syllabary had been accepted by the Cherokee National Council at its national capital in New Echota, Georgia, in 1825. The laws of the Cherokee nation were printed using the syllabary in 1826, while the bilingual, biscriptal newspaper the Cherokee Phoenix began printing in 1828 in New Echota using a newly designed typeface. In that same year, Sequoyah traveled to Washington as part of a delegation to advocate against the removal of those Cherokee still living east of the Mississippi to the Indian Territory (now eastern Oklahoma), an effort that would ultimately prove unsuccessful in light of President Andrew Jackson’s policies against Native Americans.

By this time, Sequoyah was becoming widely recognized by the American intelligentsia for his invention of the Cherokee script, the first and at the time only indigenously invented script for any people north of Mexico, but also as a public, American intellectual whose accomplishments demonstrated that Europe had no monopoly on inventive genius. This counternarrative to the myth of the indigenous primitive was never predominant, but at times, when Euro-Americans saw their interests in terms of distinguishing themselves from Europe, some might coopt Native American accomplishments by claiming them as generically American.
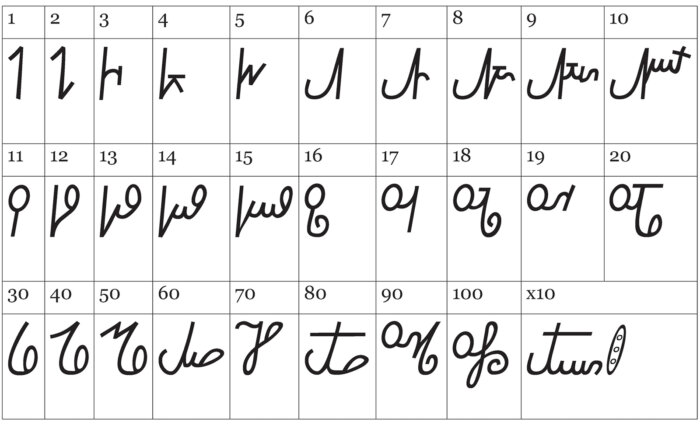
Shortly after his return from Washington, Sequoyah presented this next invention to the Cherokee National Council: a set of numeral signs. Unlike the Hindu-Arabic, or Western numerals 0123456789, Sequoyah’s numerals had principally a ciphered-additive structure. That is, instead of place value and a zero, there are separate signs for each decade and unit, which combine together, so that 67 would be the sign for 60 followed by 7, rather than 6 followed by 7 as in Western numerals. Beyond 100, the system became multiplicative-additive — instead of developing nine new signs for 100 through 900, Sequoyah invented only one, which combined with the signs for 1 through 19.
Other than in John Howard Payne’s papers containing the numerals, there is no further 19th-century direct evidence for their use, and scant evidence for their origins.
Ciphered-additive notation, though rare today, was extraordinarily widespread cross-culturally prior to the past couple of centuries. Greek, Hebrew, and Arabic alphabetic numerals are all ciphered-additive; all of the mathematics of the ancient Greeks was written down using ciphered-additive numerals, showing that they are perfectly adequate for such functions. From the Egyptian hieratic numerals used in almost all the quotidian tasks of the Egyptian state, to the traditional Sinhalese numerals of south India and Sri Lanka, or the Siniform numerals developed for the Jurchin script in 12th-century China, ciphered-additive numeration is cross-culturally recurrent. These other systems were almost entirely unknown in American intellectual life at the time. In other words, just as Sequoyah’s syllabary had no parallel among the American scripts of the time, his numerals were similarly distinct from any other local system in use.
Today the Cherokee numerals survive principally in a manuscript held at the Gilcrease Museum in Tulsa, Oklahoma, which Sequoyah wrote in late 1839 and one page of which was annotated in the English language and Western numerals by his interlocutor, the poet and dramatist John Howard Payne.

Museum, Tulsa, OK)
By this point, although the Cherokee had been displaced to Oklahoma in the American imperial project now known as the “Trail of Tears,” the syllabary itself was widely accepted — by many accounts, the Cherokee literacy rate in the syllabary was as high as Anglo-Americans’ was in English at the time. Cherokee writers engaged in a wide variety of formal and vernacular literacy practices, such as the wall inscriptions in Manitou Cave, Alabama, interpreted as relating to ceremonial activities at a time of deep cultural disruption. Yet, while Sequoyah remained a figure of prominence, his numerals were rejected by the Cherokee themselves, and all these early texts employ Western numerals when numerals are needed. Other than in John Howard Payne’s papers containing the numerals, there is no further 19th-century direct evidence for their use, and scant evidence for their origins.
Were they rejected because, as linguists Ruth Bradley Holmes and Betty Sharp Smith argue in their instructional grammar of Cherokee, “They sensibly voted Sequoyah’s numbers out, as Arabic numerals, which are simpler, were already in use”? Other than an occasional sentence in one of the many books on Cherokee writing or in biographies of Sequoyah himself, Sequoyah’s numerals are largely absent from the narrative of the syllabary and its adoption. At best, they are considered a brief and abortive attempt wisely avoided, the fruit of a “second novel syndrome” in the inventor of graphic notations.
Although the period from 1820 to 1840 is hardly the distant past, we are faced with a lack of evidence and a wealth of speculation on several critical issues. We don’t know, for example, why Sequoyah’s numerical graphemes below 20 group into fives, or why 11 through 19 have distinct graphemes even though there is no need for them once you have signs for 10 and the units one through nine. We don’t know what impetus exists for developing a ciphered-additive system where the signs for 20 through 90 have their own distinct signs, and where there is a multiplier for 10 in place of a zero, or why, given the success of Sequoyah’s syllabary, his numerals were not similarly successful. Why were they rejected by the Cherokee themselves, and why were they invented at all? The first of these questions are structural, based on the lexical and graphic properties of language and notational systems, while the latter are social and cultural.
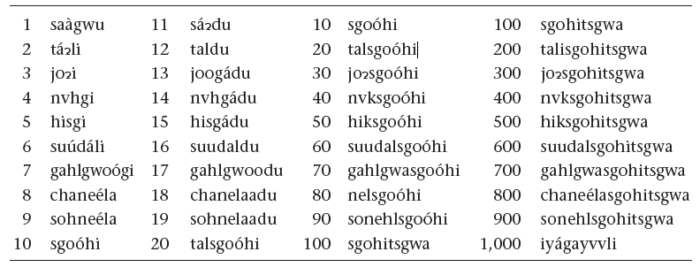
One obvious source for any structure of a numerical notation is the lexical numeral system of its inventors and its users. Perhaps some of the things that we think irregular about Sequoyah’s numerals are understandable in light the morphology of the Cherokee number words. The table of those words above has a modern linguistic rendition of the Cherokee numerals, which differs only in slight details from those presented in 19th-century grammars. We can see that with only one partial exception, the Cherokee verbal numerals are an ordinary decimal number system in which the powers of 10 (sgoóhi for ten and sgohitsgwa for hundred) are combined with the ordinary words for one through nine. The only irregularity is a common one cross-linguistically, which is that the teens from 11 through nineteen are not simply “ten one, ten two, ten three,” but use a special morpheme, du, which seems to mean “10” but is perhaps better translated as “beyond” or “added on,” with the ten elided. While these are transparent, they are irregular, just as the teens are in most Indo-European languages. This does suggest that this feature, at least, was salient to Sequoyah when inventing his numerals.
Most numerical notations do not reproduce the irregularities of their speakers’ number words. So, for instance, English eleven and twelve are opaque (they are ultimately etymologically “one left” and “two left”), but the numerals 11 and 12 follow the ordinary base-10 Western numeral system — that is, a set of signs 0123456789. But there are other cases where lexical irregularities are reproduced in a numerical notation, and the teens figure among those. In ciphered-additive Greek alphabetic numerals for 11–19, we would expect the sign for 10 (iota, I) to be followed by the signs for 1–9, because most numerical notations are written in descending order, starting with the highest powers. But, instead of writing 12 as Iβ, 10 + 2, some ancient Greek texts would write it βI, 2 + 10, to correspond with the numeral word dodeka “two (plus) ten.”
To understand the origin of Sequoyah’s numerical notation, we need more than this sort of speculation. Luckily, there is some historical evidence giving us insight into Sequoyah’s inventive process that bears directly on this question.
In 1835, Sequoyah’s cousin George Lowery, a bilingual English and Cherokee speaker who had been a major during the War of 1812, wrote a biography of Sequoyah, with an introduction and transcription by John Howard Payne (in whose papers the numerals survive), in which he discussed his kinsman’s life and practices from a culturally near and personally familiar perspective. In this passage, which has been reprinted twice since its initial publication but never analyzed, Lowery shows us the thought process of an inventor solving the numerical problems of recordkeeping in a series of steps: starting with marks for each different coin, then using tally marks alone, then tally marks crossed after every fifth number, then a special sign X for 10, then finally the fully developed numeral system we have been discussing:
But he had to give much credit; and could not remember the persons and the sums, there were so many. His alphabet had not then been thought of. He devised this mode of keeping his accounts: He would express the person by some sign or by something like a nude profile or full length likeness: and after it he would put as many large round marks as there were dollars & for smaller sums, as many smaller circles, thus: for $1.75 he would put
; but this soon confused him & then he would say for several dollars, five for instance O|||||, and so on; and after that, he would make straight marks, crossing them at every 5 as this
|||||, & if there were more tens than one, expressing each ten by a cross X. At last, he made the numbers, as he now uses them.
Bearing in mind that we really have only secondhand accounts here, we can start to see an explanation emerge in several stages. The first, Lowery reports, uses circles of different sizes for coins of different denominations — in his description, $1.00, $0.50, and $0.25, in descending order. This is not precisely a numerical system, but a very innovative iconic notation for silver coins of different sizes. The next step in Sequoyah’s thinking seems to employ these iconic depictions alongside a sort of tally-marking system, and then eventually leads to what seems to be a cumulative-additive numerical notation system with ones grouped into fives with a cross across each group of five strokes, and X marks for 10. The fact that Sequoyah eventually used X for 10 suggests, but does not prove, that he knew the Roman numerals, which would have been in general if not everyday use in American institutions at the time. Only after this sequence of inventions, each building on aspects of the previous one, did Sequoyah end up with “the numbers, as he now uses them” — in other words, the ciphered-additive numerals described above.
Thus, before he invented his numerals, and perhaps even before he had the idea for the syllabary itself, Sequoyah was thinking and representing matters visually using fives and tens. It is a small step from there to the idea of retaining a quinary visual structure in the system itself, even after he had abandoned the initial principles under which he was reckoning. We have in this passage one of the only accounts, if not from an inventor himself, then from close kin, of the stepwise and methodical invention of a numerical notation system. We are looking at a micro-scale diachronic process of invention, alteration, and replacement of different notations leading to a final ciphered-additive decimal system.
In most contexts where such problems emerge in contemporary societies, the solution is to borrow some technique or notation from others. And there were surely such models available to Sequoyah, in both the Roman numerals and the Western numerals. I do think, however, that there are good reasons why a Cherokee of inventive mind would develop a new system rather than borrowing another directly.
I return to the year where I began, 1828, and the second issue of the bilingual newspaper, the Cherokee Phoenix, published by Elias Boudinot, a Cherokee intellectual with a strong sense of national identity and whose paper embodied the aspirations of America’s indigenous elites. Boudinot starts one column by reprinting a frankly racist column on “Indian Arithmetic” from the Western Review, repeating a set of common 19th-century Anglo ideas about the mathematical language and capacities of native peoples. Immediately below this, Boudinot printed without commentary a list of three columns: the Cherokee lexical numeral words as high as one million (written in the syllabary), the Western numerals, and the Roman numerals (which in their modern forms, top out at 1,000). And immediately below that, the third and final plate in the column, he reprints a pair of quotations on the theme of revenge, and the power of silence in the face of a slight.

This is a clever piece of rhetoric, an intertextual narrative aimed directly at the growing bilingual, biscriptal Cherokee educated audience who were Boudinot’s readership. The first article sets out the dominant American narrative of the primitivity of indigenous Americans, which would have been sadly familiar to Cherokee readers. The next is a straightforward empirical demonstration of the falsehood of the first, juxtaposing the long sequence of Cherokee numeral words (though not the numeral symbols, which were not part of the typeset for the Phoenix and not much in use anyway) with the two dominant notations of the day, the Roman and Western. And, in the last text, a cheeky epigram brings the matter to a satisfying close, in case anyone was confused about this resistance narrative.

We must remember, in all of this, that the Cherokee were (and still are) a colonized people fighting for their claim to an intellectual heritage and to the right to be regarded as civilized. In a context where numeracy indexes civilization, just as literacy does, it should come as no surprise that there is a motivation to develop a local notation rather than borrow an existing one. Because numeracy is linked to the power of the state, the symbolic capital attached to numeracy is enormous. In such circumstances, many societies choose to use a borrowed system, and of course that is exactly what the Cherokee National Council decided. Where the paucity of the numerical lexicon is linked to the stereotype of “savage number,” as the historian of science Michael Barany has shown to be widespread in 19th-century Western thought, the inventive process is not merely about developing a tool, but developing an emblem that asserts the right to be considered as fully civilized.
Unfortunately, this context is also the partial answer to why, in the end, the Cherokee chose to adopt Western numerals. The power of the Western numerals is not that they are structurally superior as a notation. They have certain advantages, but in other respects (such as conciseness), the Cherokee numerals are perfectly adequate and in some cases better than the Western numerals. Rather, the Western numerals’ strength in the 19th-century American context was their ubiquity, because numeral notations are communication and representation systems first and foremost, not arithmetical systems. Almost paradoxically, Sequoyah’s numerals could not succeed because they had not yet succeeded, and came into existence in a social context where a prestigious, common notation had been adopted almost universally.

But the Cherokee syllabary is also a communication system, and it did survive, if not thrive, throughout the 19th and 20th centuries and to the present, where it is taught and used at least to a limited degree in Oklahoma and North Carolina, where most Cherokee now live. So we need some other factor, other than simple frequency dependence, to explain why the script survived but the numerals did not.
Partly the explanation may be biographical. Sequoyah’s syllabary had spread quite far by the late 1820s, at which time he began to promulgate his numerals. If the two had been invented and disseminated in tandem, their fates might have been more closely intertwined. Additionally, by the 19th century, the Western numerals were extraordinarily widespread and linked to scientific and technical practice. The Roman/Latin alphabet was predominant in American life, but was not presumed to serve as a universal script. For one thing, phonetic scripts record some signs and not others, requiring modification or replacement to serve the speakers of different languages.
Almost paradoxically, Sequoyah’s numerals could not succeed because they had not yet succeeded, and came into existence in a social context where a prestigious, common notation had been adopted almost universally.
This is not so with numerical notations, given the virtual universality of the counting numbers across linguistic and cultural divides. But even more important was the value of the Western numerals for entry into the newly developing American educational elite, something that the Cherokee middle class wanted very much. Adopting the syllabary was a nod in the direction of cultural strength and resistance to homogenizing forces. Adopting Sequoyah’s numerals, and forgoing the (by this time) universal Western numerals and the arithmetical practices that accompanied them, was a step too far. The Western numerals were regarded, by both colonizer and Cherokee, as part of a prestigious system for economic, technological, and scientific development, really only beginning to flourish in America in the 1830s and 1840s.
The failure of Sequoyah’s numerals to thrive is not the whole point, however. In short order, he invented not one but two numerical notations, the first cumulative-additive, the second ciphered-additive, neither closely resembling any possible antecedent of which he may have been aware. The invention of the Cherokee numerals was a sequence of inventive steps, built perhaps with some knowledge of other notations used locally, but progressing largely on its own terms. It survived, fortuitously, only in a handwritten manuscript shared between Sequoyah and John Howard Payne, and in the narratives of literary scholar Samuel Lorenzo Knapp, with whom Sequoyah communicated through interpreters, and Lowery who reported on the numerals’ use at one degree removed from their inventor. We should then ask: How many other numerical notations met a similar fate, with no evidence surviving at all?
Over 5,500 years of written history, there are around 100 numerical notations well-attested enough that I could describe them in my previous work, including the Cherokee case. Each of the basic structures was invented multiple times independently of one another. While, in broad strokes, the history of numerical notation converged on one overwhelmingly popular system, the Western numerals, by around 1700 or so, numerical innovation never ceased. What changed was the likelihood that a community would adopt a numerical system widely, because of the overwhelming frequency-dependent and prestige biases in favor of Western numerals.
There’s every reason to think that there are many numerical systems for which evidence does not survive — or has yet to be found.
These numerical notations confirm the vitality of the inventive spirit motivating individuals and groups in each generation to experiment with numerical forms. They should also alert us to the probability that many, many older systems have been invented and either rapidly abandoned or “outnumbered” by more widespread systems. Few or limited traces may survive of these, and we may not be looking in the right places for them. I would not be surprised if as many numerical notations have yet to be discovered as have been documented to date. Some of these systems may be truly unusual compared to those already known, but the fact that the same structures, like ciphered-additive notation, are invented time and time again suggests that we are not dealing with a situation of extreme variability.
Cases like Sequoyah’s invention and refinement demonstrate a panhuman interest in numeration, given some stimulus and interest, as well as the cognitive and notational constraints that limit human inventiveness. Most of these innovations will be short-lived, and from a long-term perspective will fail. In contexts like the modern era, where Western numerals are overwhelmingly popular, it may seem pointless to focus our attention on them. But rather than seeing these merely as “dead reckonings,” we should instead regard them as evidence of the innovative numerical capacities and interests of our species, and of the brilliant inventors whose intellect underpins them.
Stephen Chrisomalis is Associate Professor of Anthropology at Wayne State University and author of, among other books, “Reckonings: Numerals, Cognition, and History,” from which this article is adapted.



